火星探测器背后的人工智能:从原理到实战的强化学习
本文详细探讨了强化学习在火星探测器任务中的应用。从基础概念到模型设计,再到实战代码演示,我们深入分析了任务需求、环境模型构建及算法实现,提供了一个全面的强化学习案例解析,旨在推动人工智能技术在太空探索中的应用。
关注TechLead,分享AI全维度知识。作者拥有10+年互联网服务架构、AI产品研发经验、团队管理经验,同济本复旦硕,复旦机器人智能实验室成员,阿里云认证的资深架构师,项目管理专业人士,上亿营收AI产品研发负责人。

一、引言
火星,作为人类探索太空的下一个重要目标,一直吸引着科学家们的眼球。火星探测器作为探索这一未知世界的先锋,承担着巨大的任务和挑战。在这一任务中,强化学习(Reinforcement Learning, RL)作为一种智能学习方法,为火星探测器的自主决策提供了新的可能性。
强化学习,简而言之,是让计算机通过与环境的交互,自主学习如何做出最优的决策。在火星探测任务中,由于火星环境的复杂性和不确定性,传统的编程方法难以覆盖所有潜在的情况。因此,强化学习在这里扮演着至关重要的角色。它允许探测器在模拟环境中进行大量的试验和错误,从而学习如何在各种复杂环境下作出最佳决策。
这种学习过程类似于人类学习一个新技能。想象一下,当你第一次学习骑自行车时,你可能会摔倒很多次,但每次摔倒后,你都会学会一些新的技巧,比如如何保持平衡,如何调整方向。最终,这些累积的经验使你能够熟练地骑自行车。同样,在强化学习中,探测器通过与环境的不断交互,逐渐学习如何更好地执行任务。
在本文章中,我们将深入探讨强化学习在火星探测器任务中的应用。我们将从基本的强化学习概念开始,逐步深入到具体的模型设计、代码实现,以及最终的任务执行。通过这一系列的解析,我们不仅能够了解强化学习技术的细节,还能够领略到其在现实世界中的巨大潜力和应用价值。
二、强化学习基础
 在深入探讨火星探测器的案例之前,我们需要建立强化学习的基础。强化学习是一种让机器通过试错来学习如何完成复杂任务的方法。这种方法的美妙之处在于,它不是简单地告诉机器每一步该做什么,而是让机器自己发现如何达成目标。
在深入探讨火星探测器的案例之前,我们需要建立强化学习的基础。强化学习是一种让机器通过试错来学习如何完成复杂任务的方法。这种方法的美妙之处在于,它不是简单地告诉机器每一步该做什么,而是让机器自己发现如何达成目标。
强化学习的基本概念
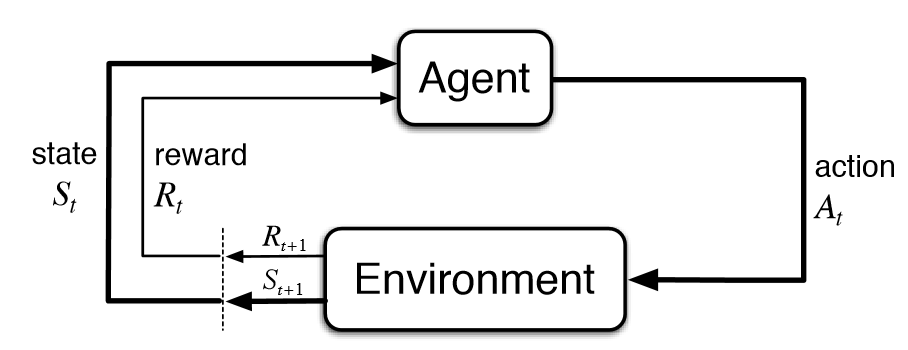 在强化学习中,有几个关键概念:
在强化学习中,有几个关键概念:
- 代理(Agent):在火星探测器的例子中,代理就是探测器本身。
- 环境(Environment):环境是代理所处的世界,即火星的表面和大气。
- 状态(State):代理在某一时间点的情况,例如探测器的位置和周围环境。
- 动作(Action):代理可以执行的操作,比如移动或者采集样本。
- 奖励(Reward):代理根据其动作获得的反馈,用于评价动作的好坏。
主要算法概述
在强化学习中,有多种算法,如Q-Learning、Deep Q-Network(DQN)、Policy Gradients等。每种算法都有其独特之处,但它们共同的目标是优化代理的行为以最大化累积奖励。
以Q-Learning为例,它是一种基于价值的方法,旨在学习一个动作价值函数(Action-Value Function),指示在特定状态下采取特定动作的预期效用。
Q-Learning 示例代码
import numpy as np
# 初始化Q表
Q = np.zeros([环境状态数, 环境动作数])
# 学习参数
学习率 = 0.8
折扣因子 = 0.95
for episode in range(总迭代次数):
状态 = 初始化环境()
while not done:
动作 = 选择动作(状态, Q) # 根据Q表或随机选择
新状态, 奖励, done, _ = 执行动作(动作)
# Q表更新
Q[状态, 动作] = Q[状态, 动作] + 学习率 * (奖励 + 折扣因子 * np.max(Q[新状态]) - Q[状态, 动作])
状态 = 新状态
环境建模与奖励设计
在火星探测器的案例中,环境建模尤为关键。我们需要准确地模拟火星的地形、大气条件等,以确保训练的有效性。奖励设计也至关重要,它直接影响着探测器学习的方向。例如,我们可能会给探测器设定奖励,以鼓励它避开危险地形或有效采集科学数据。
通过这一节的学习,我们为深入理解火星探测器案例奠定了坚实的基础。接下来,我们将探讨如何将这些基础应用于实际的火星探测任务。
三、火星探测器任务分析
 火星探测器任务,作为一项前所未有的挑战,需要在极端和未知的环境中作出精确决策。本章节将深入分析这一任务的细节,并探讨如何通过强化学习建立有效的模型和机制来解决这些挑战。
火星探测器任务,作为一项前所未有的挑战,需要在极端和未知的环境中作出精确决策。本章节将深入分析这一任务的细节,并探讨如何通过强化学习建立有效的模型和机制来解决这些挑战。
任务需求与挑战
火星探测器的主要任务包括表面探测、样本收集、数据传输等。每项任务都面临着独特的挑战,如极端温度变化、地形复杂、通讯延迟等。这些挑战要求探测器具备高度的自主性和适应性。
探测器环境建模
为了让强化学习算法能有效地学习和适应火星环境,我们首先需要构建一个准确的环境模型。这个模型需要包括:
- 地形特征:模拟火星的地形,包括平原、山脉、沙丘等。
- 环境条件:考虑温度、尘暴、太阳辐射等因素。
- 机器人状态:包括位置、能源水平、载荷等。
这个环境模型是探测器学习的“沙盒”,在这里,它可以安全地尝试和学习,而不会面临真实世界的风险。
目标设定与奖励机制
在强化学习中,明确的目标和奖励机制是至关重要的。对于火星探测器,我们可以设定如下目标和奖励:
- 目标:安全导航、有效采集样本、保持通讯等。
- 奖励:成功采集样本获得正奖励,能源消耗过大或受损获得负奖励。
这些目标和奖励构成了探测器学习的驱动力。通过不断地尝试和调整,探测器学习如何在复杂环境中实现这些目标。
层层递进的关系
在这个分析中,我们建立了一个层层递进的框架:
- 环境建模:首先,我们创建了一个模拟火星环境的详细模型。
- 目标与奖励:接着,我们定义了探测器需要实现的具体目标和相应的奖励机制。
- 学习与适应:基于这个环境和奖励系统,探测器通过强化学习算法学习如何完成任务。
这种逐步深入的方法不仅确保了强化学习算法可以有效地应用于火星探测器任务,而且还提供了一个框架,用于评估和优化探测器的行为和策略。
通过这个详尽的分析,我们为火星探测器的强化学习应用打下了坚实的基础。接下来,我们将深入探讨如何设计和实施强化学习模型,以实现这些复杂且关键的任务。
四、强化学习模型设计
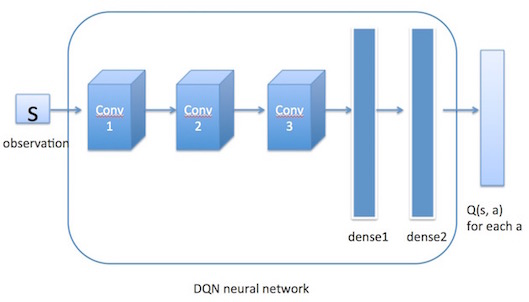 设计强化学习模型是实现火星探测器自主决策的核心。这一部分将详细介绍模型的设计过程,包括架构、状态和动作的定义,以及深度学习与强化学习的结合。
设计强化学习模型是实现火星探测器自主决策的核心。这一部分将详细介绍模型的设计过程,包括架构、状态和动作的定义,以及深度学习与强化学习的结合。
模型架构概述
在火星探测器的案例中,我们选择**深度Q网络(Deep Q-Network, DQN)**作为核心算法。DQN结合了传统的Q-Learning算法和深度神经网络,使得代理能够处理更复杂的状态空间。
DQN架构核心组件:
- 输入层:代表探测器的当前状态。
- 隐藏层:多个层次,用于提取状态的特征。
- 输出层:代表每个动作的预期回报。
状态、动作与奖励的定义
在强化学习中,状态、动作和奖励的定义至关重要。在我们的案例中:
- 状态(State):包括探测器的位置、方向、速度、能源水平等。
- 动作(Action):如移动方向、速度改变、数据采集等。
- 奖励(Reward):基于任务目标,如成功采集样本给予正奖励,能耗过大或损坏给予负奖励。
深度学习与强化学习的结合
将深度学习与强化学习结合起来,能够处理复杂的状态空间和高维动作空间。在DQN中,深度神经网络用于近似Q函数(动作价值函数),以预测在给定状态下每个动作的预期回报。
DQN模型代码示例
import torch
import torch.nn as nn
import torch.optim as optim
# 神经网络结构定义
class DQN(nn.Module):
def __init__(self, 输入状态数, 动作数):
super(DQN, self).__init__()
self.fc1 = nn.Linear(输入状态数, 50)
self.fc2 = nn.Linear(50, 50)
self.fc3 = nn.Linear(50, 动作数)
def forward(self, x):
x = torch.relu(self.fc1(x))
x = torch.relu(self.fc2(x))
return self.fc3(x)
# 实例化网络
网络 = DQN(输入状态数, 动作数)
损失函数 = nn.MSELoss()
优化器 = optim.Adam(网络.parameters(), lr=0.001)
在这个示例中,我们构建了一个简单的神经网络,具有三个全连接层。这个网络将接受探测器的状态作为输入,并输出每个动作的预期价值。
通过这一节的设计和代码实现,我们为火星探测器的自主决策打下了坚实的基础。在接下来的章节中,我们将展示如何使用这个模型进行实际的训练和评估。
五、完整实战代码演示
在这一部分,我们将演示一套完整的实战代码,用于火星探测器任务的强化学习训练。这套代码将包括环境设置、模型定义、训练循环,以及模型评估的步骤。
1. 环境设置
首先,我们需要设置模拟火星环境。这里假设我们已经有一个模拟环境,它能够提供状态信息和接受动作输入。
import gym # 使用gym库来创建模拟环境
# 假设'火星探测器环境'是已经定义好的环境
环境 = gym.make('火星探测器环境')
2. DQN模型定义
接下来,我们定义深度Q网络(DQN)模型。这个模型将用于学习在给定状态下执行哪个动作可以获得最大的回报。
class DQN(nn.Module):
def __init__(self, 输入状态数, 动作数):
super(DQN, self).__init__()
# 定义网络层
self.fc1 = nn.Linear(输入状态数, 64)
self.fc2 = nn.Linear(64, 64)
self.fc3 = nn.Linear(64, 动作数)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
return self.fc3(x)
输入状态数 = 环境.observation_space.shape[0]
动作数 = 环境.action_space.n
网络 = DQN(输入状态数, 动作数)
3. 训练过程
在训练过程中,我们将让探测器在模拟环境中执行动作,并根据反馈更新网络。
def 选择动作(状态, epsilon):
if np.random.rand() < epsilon:
return 环境.action_space.sample() # 探索
else:
with torch.no_grad():
return 网络(torch.from_numpy(状态).float()).max(0)[1].item() # 利用
# 训练参数
epochs = 1000
epsilon = 1.0
epsilon_decay = 0.995
min_epsilon = 0.01
学习率 = 0.001
优化器 = optim.Adam(网络.parameters(), lr=学习率)
for epoch in range(epochs):
状态 = 环境.reset()
总奖励 = 0
while True:
动作 = 选择动作(状态, epsilon)
新状态, 奖励, done, _ = 环境.step(动作)
总奖励 += 奖励
# Q-Learning更新
目标 = 奖励 + (0.99 * 网络(torch.from_numpy(新状态).float()).max(0)[0] if not done else 0)
当前Q值 = 网络(torch.from_numpy(状态).float())[动作]
loss = F.mse_loss(当前Q值, torch.tensor([目标]))
优化器.zero_grad()
loss.backward()
优化器.step()
if done:
break
状态 = 新状态
epsilon = max(epsilon * epsilon_decay, min_epsilon)
print(f"Epoch: {epoch}, Total Reward: {总奖励}")
4. 模型评估
最后,我们对训练好的模型进行评估,以验证其性能。
def 评估模型(环境, 网络, 评估次数=10):
总奖励 = 0
for _ in range(评估次数):
状态 = 环境.reset()
while True:
动作 = 网络(torch.from_numpy(状态).float()).max(0
)[1].item()
状态, 奖励, done, _ = 环境.step(动作)
总奖励 += 奖励
if done:
break
平均奖励 = 总奖励 / 评估次数
return 平均奖励
评估结果 = 评估模型(环境, 网络)
print(f"平均奖励: {评估结果}")
以上是火星探测器任务的强化学习实战代码演示。通过这个例子,我们展示了如何从环境设置、模型定义到训练和评估的整个流程,为实现火星探测器的自主决策提供了一个详细的指南。
六、总结
经过前面几个章节的深入探讨和实战演示,我们现在对于如何应用强化学习于火星探测器的任务有了全面的了解。此篇章节的总结旨在回顾我们所学的内容,并提出一些对未来研究和应用的展望。
回顾核心要点
-
强化学习的基础:我们介绍了强化学习的基本概念,包括代理、环境、状态、动作和奖励,并概述了主要的强化学习算法,为后续内容打下基础。
-
火星探测器任务分析:在这一部分,我们分析了火星探测器任务的需求和挑战,包括环境建模、目标设定与奖励机制的设计,这是强化学习模型成功的关键。
-
模型设计与实战代码:详细介绍了强化学习模型的设计,特别是深度Q网络(DQN)的应用。我们还提供了一套完整的实战代码,包括环境设置、模型训练和评估,使理论得以应用于实践。
展望未来
尽管我们在模拟环境中取得了进展,但在实际应用中,火星探测器面临的挑战要复杂得多。未来的研究可以聚焦于以下几个方面:
- 环境模型的改进:更加精确地模拟火星的环境,包括更多变化和未知因素。
- 算法的进一步发展:探索更先进的强化学习算法,提高学习效率和适应性。
- 硬件与软件的协同:优化探测器的硬件设计以更好地适应强化学习算法,提高整体性能。
- 实际任务应用:在模拟环境中验证的算法需要在实际火星探测任务中得到测试和应用。
结语
强化学习在火星探测器任务中的应用展示了人工智能技术在解决复杂、现实世界问题中的巨大潜力。通过不断的研究和实践,我们不仅能推动科技的发展,还能为人类的太空探索事业做出贡献。希望这篇文章能激发更多热情和兴趣,促进人工智能和太空探索领域的进一步研究和发展。
关注TechLead,分享AI全维度知识。作者拥有10+年互联网服务架构、AI产品研发经验、团队管理经验,同济本复旦硕,复旦机器人智能实验室成员,阿里云认证的资深架构师,项目管理专业人士,上亿营收AI产品研发负责人。 如有帮助,请多关注 TeahLead KrisChang,10+年的互联网和人工智能从业经验,10年+技术和业务团队管理经验,同济软件工程本科,复旦工程管理硕士,阿里云认证云服务资深架构师,上亿营收AI产品业务负责人。
|
- 上一条: 测试用例设计方法六脉神剑——第三剑:倚天屠龙,正交试验冲锋 | 京东物流技术团队 2023-12-12
- 下一条: 火星探测器背后的人工智能:从原理到实战的强化学习 2023-12-12
- 大模型时代的人工智能+大数据平台,加速创新涌现 2023-10-31
- 百度工程师浅析强化学习 2023-08-18
- 机器学习-逻辑回归:从技术原理到案例实战 2023-12-06
- 人工智能 、机器学习、深度学习、神经网络,都有什么区别? 2021-10-13
- 强化学习的一周「GitHub 热点速览」 2023-10-23










