【深度学习编译】多面体模型编译：以优化简单的两层循环代码为例

文 @ 小 P 的小胡易生

 

0 背景

在编译器领域，多层 for 循环的代码优化往往是编译优化工作的重点内容。在深度学习编译器这一细分领域，大多神经网络中，多层 for 循环的算子占比多达一半以上。

因此，对这类代码的优化极其重要。优化手段之一是调整 for 循环语句中的每一个实例的执行顺序，即调度方式，使得新调度下的 for 循环代码有更好的局部性和并行性。

多面体模型算法的思想是：

• 将多层 for 循环视为多维空间。
• 通过静态分析和编译优化算法，对原目标程序进行空间变换。
• 最终将其优化为一个有较好局部性和并行性的新程序。

 

1 整体流程

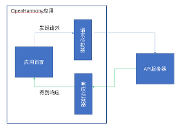
多面体模型算法的整体流程依次包括以下四个主要部分：

• 建模抽象
• 依赖分析
• 调度变换
• 代码生成

下面对这四个部分逐一进行分析。

1.1 示例代码

本文以如下简单的两层 for 循环代码为例[1]，进行多面体模型优化算法的推理。

 

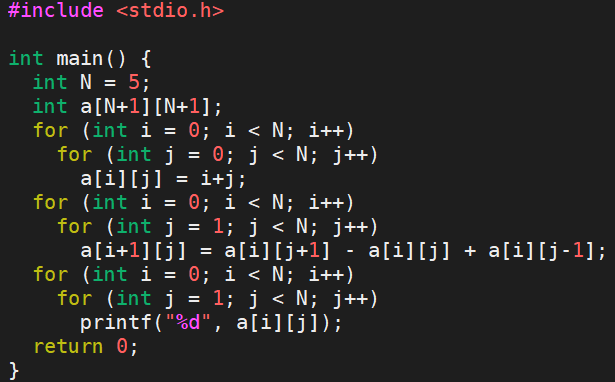
2 建模抽象

首先，本文提出调度树 (Schedule Tree) 的概念：

Schedule Tree 是一种树形的关于调度执行顺序的表示方法，由节点和边组成。它只包含 instances 的取值范围和执行顺序，而没有内存的读写信息。

在上一小节给出的示例代码中，我们针对其核心的计算部分，分析其 Schedule Tree：

此代码的核心计算部分包括 i 和 j 两层循环。计算式中由 i 和 j 所囊括的所有可以取到的值（如 i 从 0 到 N-1，j 从 0 到 N-1），整个空间成为 Schedule Tree 的域 (domain) 部分。

对于最外层循环 i 层，称为 Schedule 1。对于第二层循环 j 层，即第二层，称为 Schedule 2。

Domain 与 Schedule 1 的连接关系称为第一层次的 Child 1；Schedule 1 与 Schedule 2 的连接关系称为第二层次的 Child 2。

将上述内容用程序化语言[2]描述出来是：

 

3 依赖分析

3.1 概念说明

第二步是对示例代码进行依赖分析。为了方便理解，本文将此代码中所有的实例全部列出，如下：

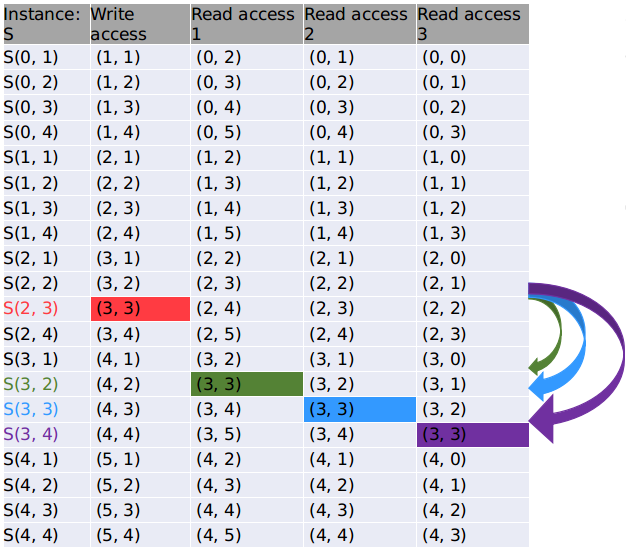
再把所有涉及到二维数组 a 中相同内存位置的实例全部找出进行分析。这里我们选择 a[3][3] 这块内存进行分析。有 S(2, 3), S(3, 2), S(3, 3), S(3, 4) 四个实例与之相关，如上图。

由于原始程序中各实例间有一定的执行顺序要求，如需要先执行实例 S(2, 3)，完成对数组 a[3][3] 的写入步骤后，才能再执行实例 S(3, 2), S(3, 3), S(3, 4) 这三个对数组 a[3][3] 的读取。换句话说，实例 S(3, 2), S(3, 3), S(3, 4) 的执行依赖于实例 S(2, 3) 的执行。上图中绿、蓝、紫三条弧线描述了这样的依赖关系。对于数组 a 中其他元素的读写，也会产生同样的依赖关系。

基于此，本文构建出一幅依赖关系图，如下：

红色圈中的实例 S(2,3) 需要先执行；而指向它的三条箭头则表示依赖它的三个实例与之的依赖关系。

另外，我们可以看出，由于此图中依赖关系（即实例执行先后顺序）的限制，导致了 i 方向上必须要依次执行，且 i 方向与 j 方向的局部性不好（即当 i 或 j 取很大的值时，容易 cache miss）。

3.2 计算步骤

有了上一小节的概念说明，如何计算输入程序中的依赖关系也变得容易起来。

计算步骤分为两步：

1. 本示例中，目标程序计算代码读取数组 a[i][j+1], a[i][j], a[j][j-1]，写入数组 a[i+1][j]。通过静态分析算法，获取目标程序的读内存和写内存的关系，如下：

2. 通过依赖分析算法，根据第一个模块收集到的调度顺序和本模块第一步收集到的内存读写关系，计算出目标程序的数据流依赖。原始程序中有如下三条依赖关系：

 

4 调度变换

4.1 概念说明

在此模块中，本文通过一维仿射变换的方式，将原始程序中的调度顺序映射为一个调度空间。对前两个模块收集到的信息进行变换操作，得到一个新空间，及其基向量。

\( \phi(v) = \vec{h} * \vec{v}, \vec{v} = \begin{pmatrix} i \ j \end{pmatrix} \)

其中向量 \(\vec{h}\) 为变换后超平面的法向量。这种变换方式称为多面体模型变换，是一个针对变换函数的系数求最优解的过程。

下图给出了将原始代码对应的调度空间转变为新调度空间的一种可能情形。

4.2 理论计算通式

本文将上一小节中提到的概念进行扩展：对于多层 for 循环视为多个维度的 \(n\) 维空间，对此 \(n\) 维空间进行 \(n\) 维仿射变换；也可以理解为针对每个维度进行一维仿射变换，总共进行 \(n\) 次变换。这种运算得到的结果即对目标程序的 \(n\) 个 for 循环完成了多面体模型的变换操作。其通式[3]如下：

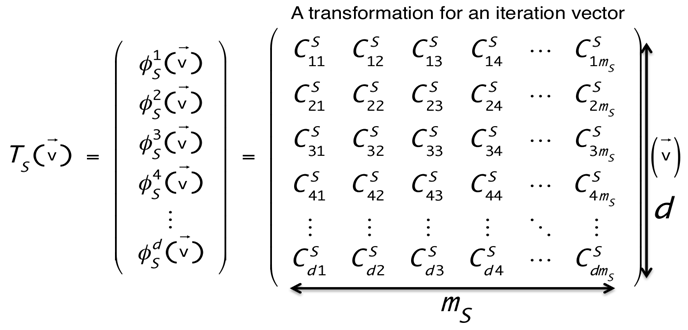
其中，\(m_{S}\) 表示循环变量的个数（即原空间维数），\(d\) 表示变换后的程序中 for 循环个数（即仿射超平面数），系数矩阵中每一行都是一个仿射超平面的法向量。

上述通式即为多个仿射超平面或多个一维仿射变换的组合。最终我们要逐行求解系数矩阵。

4.3 限制条件

为了保证变换之后的结果仍旧正确，此变换需要满足一定的限制条件。

其中限制条件的下界有两个：

1. 需要满足依赖基本定理，即变换前后调度执行顺序不变。用向量 \(\vec{s}\) 表示源实例 (source instance)，用向量 \(\vec{t}\) 表示目的实例 (target instance)。 变换前满足目的实例的字典序大于源实例，即先执行源实例，再执行目的实例。用如下公式表示： \(\)

\(lex(\vec{t} - \vec{s}) >= 0\)

则变换后仍需要满足先执行源实例，再执行目的实例，即：

\( \delta(\vec{s}, \vec{t}) = \phi S_j(\vec{t}) - \phi S_i(\vec{s}) >= 0\)

将此公式展开为： \(\)

\( (C_{1}^{S}, C_{2}^{S}, \cdots, C_{m_{S}}^{S}) * \vec{t} - (C_{1}^{S}, C_{2}^{S}, \cdots, C_{m_{S}}^{S}) * \vec{s} = (C_{1}^{S}, C_{2}^{S}, \cdots, C_{m_{S}}^{S}) * (\vec{t} - \vec{s}) >= 0\)

这里的向量 \(\vec{t}\) 与向量 \(\vec{s}\) 的差也可以视为 “依赖分析” 一节中计算出来的依赖向量，指的都是从源实例到目的实例这一执行顺序。

2. 需要满足通式的结果无平凡解，即需要保证系数不全为 0：\(\)

\(​ \sum_{i=1}^{m_S} C_i^S >= 1 ​\)

其中限制条件的上界有一个： 由于 for 循环中的循环变量自身有上界，因此总是存在： \(\)

\(​ v(\vec{n}) = \vec{u} * \vec{n} + w ​\)

使得此式满足：

\(​ v(\vec{n}) - \delta(\vec{s}, \vec{t}) = v(\vec{n}) - (\phi S_j(\vec{t}) - \phi S_i(\vec{s})) >= 0 ​\)

\(\)其中向量 \(\vec{n}\) 是循环变量的上界符号常数（如原始程序中的 \(N\)）的系数向量，\(k\) 表示程序中参数的个数。向量 \(\vec{u}\) 和标量 \(w\) 为构造出来的未知变量。

 

对于本文给出的示例程序，所有需要满足的限制条件如下：

\(\begin{cases} (C_1, C_2)*\begin{pmatrix} 1 \\ 1 \end{pmatrix} = C_1+ C_2 >= 0 \\ (C_1, C_2)*\begin{pmatrix} 1 \\ 0 \end{pmatrix} = C_1 >= 0 \\ (C_1, C_2)*\begin{pmatrix} 1 \\ -1 \end{pmatrix} = C_1 - C_2 >= 0 \\ \sum_{i=1}^{2} C_i = C_1 + C_2 >= 1 \\ u * N + w -(C_1, C_2)*\begin{pmatrix} 1 \\ 1 \end{pmatrix} = u * N + w -C_1 - C_2 >= 0 \\ u * N + w -(C_1, C_2)*\begin{pmatrix} 1 \\ 0 \end{pmatrix} = u * N + w - C_1 >= 0 \\ u * N + w -(C_1, C_2)*\begin{pmatrix} 1 \\ -1 \end{pmatrix} = u * N + w - C_1 + C_2 >= 0 \\ \end{cases}\)

 

4.4 代价函数

对于这一节提出的最优化问题，本文提出了如下代价函数：

\( \delta(\vec{s}, \vec{t}) = \phi S(\vec{t}) - \phi S(\vec{s}) \)

此代价函数表示如下两层含义：

1. 当一维仿射变换对应不同超平面上的循环迭代串行执行时，该函数代表了数据被重用的时间间隔。\(\delta\) 越大，局部性越差。

2. 当并行执行时，该函数则代表了 \(t\) 时刻到 \(t+1\) 时刻多个核之间的通信量，即计算 \(t+1\) 时刻需要从 \(t\) 时刻输入的数据量。\(\delta\) 越大，核间需要传输的数据量越多。

 

4.5 目标函数

对于这一节提出的最优化问题，本文提出了如下目标函数：

\( \underset{\min}{lex} (\vec{u}, w, C_1^S, C_2^S, \cdots, C_{ms}^S) \)

即在满足所有限制条件的情况下，依次寻找各个最小的系数。

 

5 计算结果

对于本文中所示例的原始程序，对其进行多面体模型算法进行优化，计算结果为

\(\begin{cases} (u, w, C_{11}, C_{12}) = (0, 1, 1, 0) \\ (u, w, C_{21}, C_{22}) = (0, 2, 1, 1) \\ \end{cases}\)

带入通式中得到：

\( T_S(\vec{v}) = \begin{pmatrix} i_{new}\\j_{new}\end{pmatrix} = \begin{pmatrix} 1, 0 \\1, 1 \end{pmatrix} * \begin{pmatrix} i_{old} \ j_{old} \end{pmatrix} \)

即

\( i_{new} = i_{old} \ j_{new} = i_{old} + j_{old} \)

将此计算结果变量带入到目标程序中，得到一个新的程序[4]，如下：

 

6 结果分析

对于此算法得到的结果进行分析，新程序的全部实例如下：

其对应的依赖关系图为：

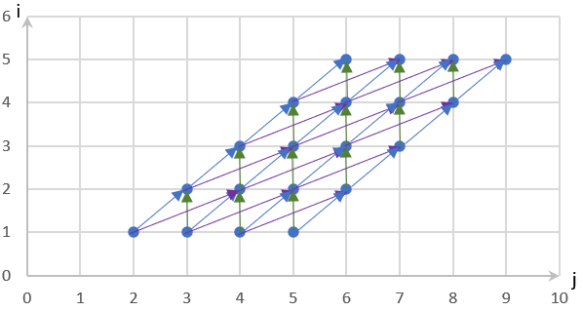
从依赖关系图上看，新程序的实例依赖关系解除了 j 方向的负依赖（即原始程序的依赖关系图中箭头方向向左的依赖）；而 j 方向仍无依赖，即可以按照 j 方向进行并行计算。

进一步，对于多核处理器，增加了下图中虚线方向的并行。且更方便 tile 分块（以绿色块为例）：按照虚线方向并行或绿色块 tile 后并行，代码的局部性更好。

 

7 总结

本文给出多面体模型优化算法的基础流程，并给出了一个简单程序在 CPU 平台上的优化过程。经过多面体模型优化，示例代码的并行程度得到了一定程度的提高，局部性也得到了增强。

本文证明了多面体模型算法的可行性和有效性，也提供了后续实现多面体模型算法的技术和理论基础。

如有谬误和歧义，请联系作者。感谢！

 

参考与引用

---

 

感谢阅读，欢迎在评论区留言讨论哦~